Backup/Export ข้อมูลใน Zotero

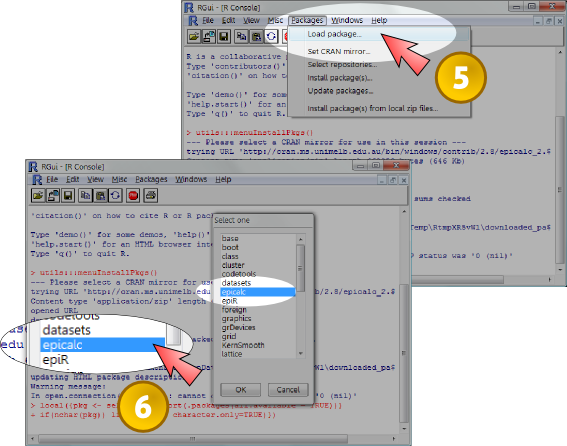
พอดีมีผู้สนใจถามมาเกี่ยวกับเรื่องการ Backup ข้อมูลใน Zotero นะครับ ผมเลยเอามาเขียนให้อ่านกันโดยทั่วๆ ใครที่ยังไม่รู้จัก Zotero ผมแนะนำให้ลองใช้ดู ยังไงลองอ่านเรื่องเกี่ยวกับ Zotero ได้ในหน้านี้นะครับ

โดยปกติแล้ว Zotero นั้นจะเก็บข้อมูลต่างๆ ที่เราได้ทำการบันทึก ทั้งในเรื่องของรายการ และไฟล์แนบ (เช่นพวก PDF หรือ Snapshot ทั้งหลาย) เอาไว้ในโฟลเดอร์ Zotero ที่อยู่ย่อยของโฟลเดอร์ Profile ของ Firefox อีกที โดยส่วนใหญ่ของผู้ใช้วินโดวส์ Vista/7 ก็จะอยู่ลึกมาก (เช่นของผมนั้นอยู่ที่ C:\Users\Pawin Numthavaj\AppData\Roaming\Mozilla\Firefox\Profiles\oc7s70ri.default\zotero\storage เป็นต้น) สำหรับวิธีการหาโฟลเดอร์นี้โดยง่ายก็คือการเข้าไปที่ Preference -> Advance -> Show Data Directory ดังวิธีต่อไปนี้ครับ

1. คลิ๊กตรงรูปเฟืองใน Zotero


2. เลือก Preferences


3. คลิ๊กตรง Advanced


4. คลิ๊กที่ Show Data Directory

หน้าตาของโฟลเดอร์ที่สามารถ Backup ไว้ก็จะปรากฏออกมาครับ เราสามารถคัดลอกทั้งหมดนี้ไปเก็บไว้ต่างหาก ไว้เผื่อเวลาที่เกิดความเสียหายกับเครื่องได้เลยครับ

โดยถ้าเราเกิดทำเครื่องพังไป เราสามารถคัดลอกไฟล์ทั้งหมดที่เคย Backup เอาไว้กลับมาไว้ตรงโฟลเดอร์นี้ (เปิดด้วยวิธีเดียวกัน) สิ่งต่างๆที่เราเคยทำไว้ก็จะกลับมาได้ทั้งหมดครับ

นอกจากวิธีที่จะ Backup ทั้งหมดแล้วเรายังสามารถเลือก Backup เป็นส่วนๆ ได้ด้วยการอาศัยคำสั่ง Export ตามขั้นตอนต่อไปนี้ครับ

1. คลิ๊กขวาตรงโฟลเดอร์ที่ต้องการส่งออก/Backup (จะคลิ๊กขวาทั้ง My Library เลยก็ได้ไม่ผิดกติกา)


2. เลือก Export Collection


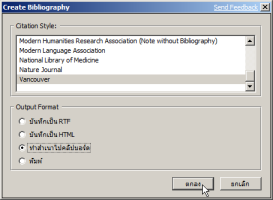
3. เลือก Format เป็น Zotero RDF ถ้าต้องการเก็บไฟล์ที่แนบเอาไว้ด้วยก็อย่าลืมติ๊กเลือก Export Files นะครับ


4. พิมพ์ชื่อที่ต้องการ แล้วกด Save

เมื่อส่งออกไปแล้วจะเป็นโฟลเดอร์ที่เก็บไว้ครับ ถ้าเราต้องการนำเข้าก็ง่ายๆ แค่เลือก Import จากเมนูเฟืองเท่านั้นเองครับ

 

แต่เท่านั้นยังไม่พอ (ดูมันง่ายไปไหม) ผมแนะนำบริการใหม่ที่จะมีมาอวดโฉมกันใน Zotero 2.0 ซึ่งยังไม่คลอด แต่มีให้ทดลองใช้กันก่อน (ผมใช้อยู่ก็พบว่าไม่เกิดปัญหาอะไรนะครับ) โดยเราสามารถที่จะ Sync สิ่งต่างๆ ที่อยู่ในเครื่องเรา ไปเก็บเอาไว้ในฐานข้อมูลออนไลน์ได้เลยทีเดียว

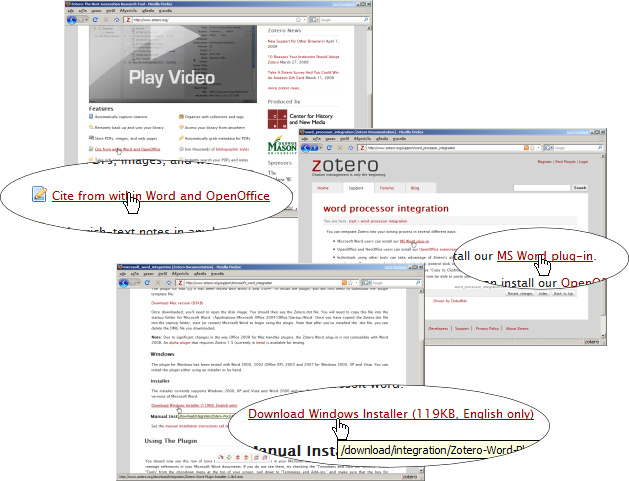
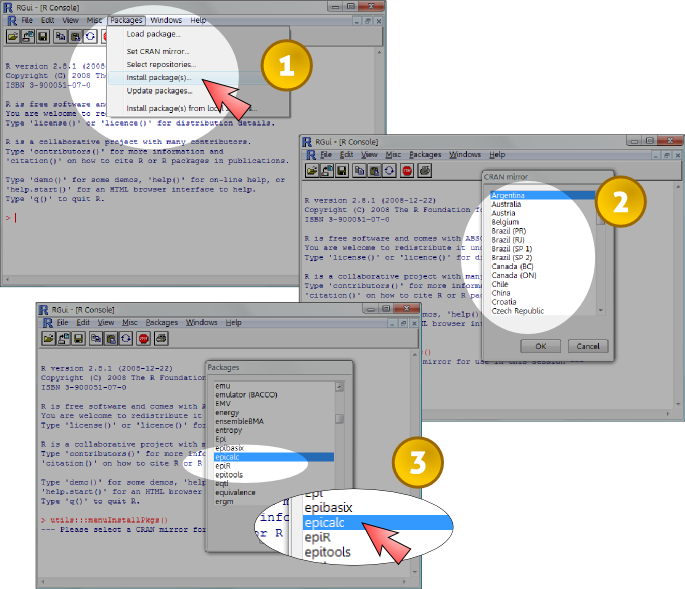
ก่อนอื่นก็ต้องขอให้ติดตั้ง Zotero รุ่น 2.0 กันก่อนครับ ขั้นตอนก็ง่ายๆ เหมือนรุ่น 1.0 เพียงเข้าไปที่เว็บ http://www.zotero.org แล้วเลือกปุ่ม try out 2.0 beta รอสักครู่ เลือก Install และรอโหลดก็จะได้มาใช้กันแล้ว (ใครกดแล้วมันเงียบแต่มีปุ่มขึ้นให้กด Allow ก็ให้กดไปนะครับ)

ถ้าอัพเกรดมาจากรุ่น 1.0 ก็จะมีให้รออัพเกรดเล็กน้อย

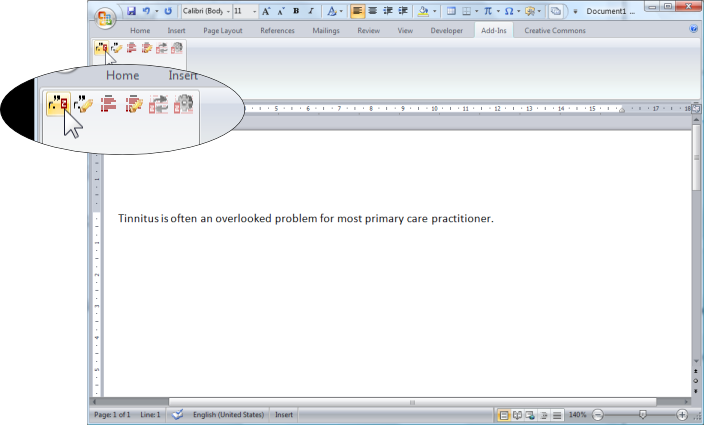
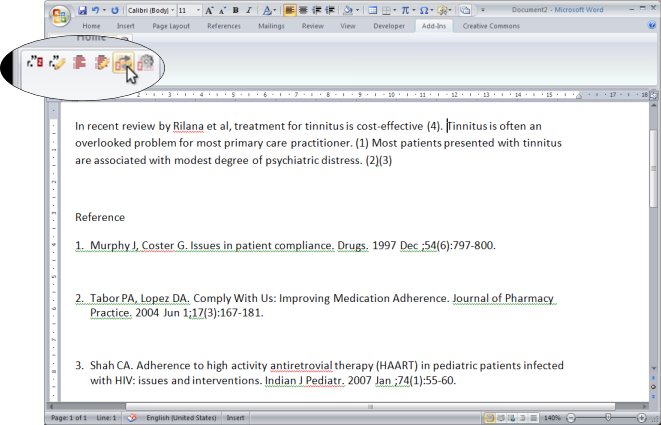
หลังจากเปิดมาแล้วเราจะพบกับหน้าตาที่แปลกไปกว่าเดิมเล็กน้อย และที่ผมอยากให้สนใจคือปุ่มรูปลูกศรโค้งๆ ด้านขวามือนี่ละครับ

ถ้าเรากดปุ่มนี้ เบื้องต้นมันจะเข้าไปที่หน้า Sync ของ Zotero ให้กรอกพวก User Name, Password ของ Zotero ถ้าใครยังไม่มีก็สามารถเข้าไปสร้างแอคเค้าท์กันได้ตามลิงค์ Create Account ที่อยู่ในหน้านั้นเลยครับ

อนึ่ง หลังจากทำการ Sync แล้วรายการต่างๆ ของเรานั้นจะไปอยู่บนคอมพิวเตอร์เซอร์เวอร์ของ Zotero ด้วย โดยถ้าเราทำในคอมเราหายและต้องการให้ Sync ย้อนกลับมาที่เครื่องเรา ก็เพียงเลือก Restore from Zotero Server เท่านั้นเองครับ

ดูง่ายดีไหมครับ นอกจากนี้แล้ว หากเราเข้าไปยังเว็บ http://www.zotero.org แล้วเลือก Login ตาม User Name ที่เราสร้างไว้ รายการต่างๆ ของเราก็จะอยู่ในนั้นด้วยครับ! ซึ่งรายการที่อยู่บนเว็บนี้ยังรวมทั้ง PDF ที่เก็บไว้ใน Library ด้วยนะครับ แต่สำหรับบริการฟรีนั้นจะเก็บได้แค่ 100 เมกะไบต์ (นับเฉพาะไฟล์ต่างๆ ไม่นับจำนวน Reference) ถ้าต้องการเก็บเพิ่มเติมก็สามารถซื้อเพิ่มกันได้ครับ

ยังไงลองใช้กันดูนะครับ :)

Clinical Epidemiology Short Course

พักนี้ไม่ค่อยจะว่างเขียนเรื่องใหม่ๆ ให้อ่านกันเท่าไหร่ครับ

แต่ว่าพอดีทางหน่วยระบาดวิทยาคลินิกและชีวสถิติ รามาฯ ที่ผมเรียน (และทำงาน) ได้อัดเทปการสอนเกี่ยวกับคอร์สสำหรับ Resident ที่ว่าด้วยเรื่อง Epidemiology และ Statistics ครับ ก็เลยเอามาฝากกัน

ไปดูกันได้ที่หน้าเว็บของหน่วยฯ ได้ที่นี่เลยครับ: http://www.ra.mahidol.ac.th/en/dpt/CEB/shortcourse_residenten

ชนิดของตัวแปร

ข้อมูลที่เกิดขึ้นจากการวัด ที่แตกต่างกันไปในแต่ละคน ในทางการวิจัยเราจะเรียกมันว่า "ตัวแปร" (variable) ครับ เช่นง่ายๆ ผมทำสำรวจการเรื่องการได้ยินในนักดนตรี ตัวแปรพวกนี้ที่เจอบ่อยๆ ก็เช่น เพศ อายุ นอกจากนี้ก็จะเป็นตัวแปรที่เกี่ยวข้องกับงานวิจัยของเราครับ นั่นคือของผมก็อาจจะเป็น ระดับการได้ยินเฉลี่ยในหูซ้ายและหูขวาในปัจจุบัน, ระดับเสียงที่ได้ยินโดยเฉลี่ยต่อวัน, จำนวนชั่วโมงที่เล่นเพลง, รูปแบบเพลงที่ชอบเล่น, ประวัติเคยใช้เครื่องช่วยฟังมาก่อนหรือไม่, ประวัติการได้ยินผิดปกติในญาติ

ตัวแปรต่างๆ เราจะต้องทำความเข้าใจมันก่อนว่ามันเป็นตัวแปรแบบไหน ทั้งนี้เพื่อที่จะได้รู้ต่อไปว่า ควรจะแปลความหมายมันอย่างไร จะแสดงผลเป็นกราฟแบบไหน จะใช้การทดสอบทางสถิติตัวไหนมาทดสอบความแตกต่างในแต่ละกลุ่ม และจะแปลความหมายผลการทดสอบนั้นอย่างไรครับ

ตัวแปรที่พบกันบ่อยๆ นั้นสามารถแยกได้สองกลุ่มใหญ่ๆ นั่นคือ

• ตัวแปรแบบกลุ่ม (Categorical Data) พวกนี้ แต่ละกลุ่มก็มีความหมายของตัวมันเอง ซึ่งแบ่งย่อยได้สองกลุ่ม คือ
  
  
  • Nominal แต่ละกลุ่มเป็นอิสระต่อกัน ไม่ค่อยเกี่ยวกัน ไม่เป็นลำดับ (order) เช่น เพศ รูปแบบเพลงที่ชอบเล่น (พูดง่ายๆ คือไม่ใช่ว่าเพศหญิงมีค่ามากกว่าเพศชาย หรือเพลงร็อกมีความมายมากกว่าเพลงเพื่อชีวิต) สำหรับตัวแปรชนิดนี้ ถ้ามีสองคำตอบ เช่น ใช่ หรือไม่ใช่ จะเรียกว่าเป็น Dichotomous หรือ Binary ครับ เช่นในตัวอย่างที่ผมยกนั้นคือตัวแปรที่บอกว่า "เคยใช้เครื่องช่วยฟังมาก่อนหรือไม่" นั้นคำตอบมีแค่ "ใช่" กับ "ไม่ใช่" เป็นต้นครับ
  
  
  • Ordinal พวกนี้จะมีลำดับขั้น แต่ไม่สามารถบอกได้ว่าขั้นไหนมากกว่าขั้นไหนได้อย่างชัดเจน (คือแต่ละขั้นมันอาจไม่เท่ากันก็ได้) ยกตัวอย่างพวกนี้เช่น ระดับความดังของเสียงผิดปกติของหัวใจ (เกรด I, II, III, ฯลฯ) ก็ไม่ได้หมายความว่า เสียงหัวใจเกรด II มากกว่าเกรด I ซักเท่าไหร่ เป็นต้น
  
  
  
  


• ตัวแปรแบบช่วง (Interval Data) พวกนี้มักจะมีลำดับขั้นของมัน และเป็นลำดับขั้นที่แบ่งอย่างเท่าๆ พอๆ กัน แบ่งออกอีกเป็นสองกลุ่มครับ
  
  
  • Continuous ง่ายๆ คือพวกนี้เป็นตัวแปรที่สามารถจุดย่อยลงไปได้อีกเรื่อยๆ เช่น ระดับการได้ยินมีทั้งได้ยินที่ 25 dB, ได้ยินที่ 40.0056 dB เป็นต้น บางคนยังได้แยกตัวแปรที่มี "ศูนย์ที่แปลว่าไม่มี" ออกไปอีกเรียกว่า Ratio ครับ เช่นความยาวของขน (ยาว=0 หมายถึงไม่มีความยาวจริงๆ) เป็นต้น
  
  
  • Discrete คือเป็นสเกลที่แบ่งชัดเจน พวกนี้มีระยะห่างกันชัด (หรือสเกลแต่ละช่วงไฟมันเท่ากัน) ครับ เช่น จำนวนบุตร ก็ตอบ 1 2 3 4 ไม่มีใครตอบ 1.25 และเราก็รู้ว่า 2 มากกว่า 1 อยู่ 1 คน, 4 มากกว่า 1 อยู่ 3 คน เป็นต้นครับ
  
  
  
  

พอจะเข้าใจไหมครับ ยังไงลองมาคิดดูนะครับ ว่าตัวแปรต่อไปนี้เป็นตัวแปรแบบไหน

• น้ำหนักของผู้ป่วย เช่น 60kg, 50.25kg, 40.7kg, ...


• จำนวนบล็อกที่ผมเขียนในแต่ละเดือน เช่น 0, 1, 3, ...


• จำนวนก้อนมะเร็งที่คอ เช่น 1 ก้อน, 2 ก้อน, 0 ก้อน, ...


• ชนิดของมะเร็งที่ศีรษะที่พบในคนไทย เช่น มะเร็งโพรงจมูก, มะเร็งต่อมน้ำลาย, มะเร็งกล่องเสียง...


• ลักษณะของเม็ดเลือดแดงที่ผิดปกติ เช่น 1+, 3+, 4+, ...

.

.

.

.

.

.

เฉลยนะครับ

• น้ำหนัก เป็น continuous interval data ครับ เพราะมันสามารถจุดย่อยลงไปได้เรื่อยๆ และมีความหมาย นอกจากนี้ถ้าแยกย่อย มันก็คือ ratio เพราะมันมี 0 แท้จริงครับ (0 kg = ไม่มีน้ำหนัก)


• จำนวนบล็อก เป็น discrete interval data ครับ เพราะไม่มีเขียนบล็อก 1.05 บล็อกแน่ๆ แต่ความแตกต่างระหว่างเขียน 3 กับ 2 บล็อก มันเหมือนกันกับความแตกต่างระหว่างเขียน 8 กับ 7 บล็อก (นั่นคือ สเกลมันเท่ากันตลอดนั่นเอง)


• จำนวนก้อนมะเร็งที่คอ เป็น discrete interval data เหมือนกัน


• ชนิดของมะเร็ง เป็น nominal เพราะไม่รู้ว่าจะเรียงมะเร็งอันไหนมาก่อนมาหลังดี มันก็สำคัญเท่าๆ กันไปหมด


• ลักษณะของเม็ดเลือดแดง เป็น ordinal ครับเพราะว่า เรียงได้ 0 1+ 2+ 3+ 4+ แต่ว่า 1+ เทียบกับกับ 0 อาจจะไม่เท่ากับ 4+ เทียบ 3+

งงไหมครับ จริงๆ รู้แค่ว่าเป็น continuous หรือ categorical ก็เพียงพอต่อการเลือกสถิติเข้าใช้ครับ ไว้ต่อไปผมจะเขียนเรื่องที่เกี่ยวข้องนะครับ :)

คำนวณ Sample Size ใน RCT

ปัญหาอย่างหนึ่งที่ผู้ทำวิจัยเกือบทุกคนจะต้องเจอ คือการคำนวณหาขนาดของกลุ่มตัวอย่าง (Sample Size) ที่จะทำการวิจัยครับ

ทำไมเราจึงต้องคำนวณขนาดของกลุ่มตัวอย่าง? นั่นเป็นเพราะว่าเราต้องการจะเก็บข้อมูลอย่างมีประสิทธิภาพให้ได้มากที่สุดครับ นั่นหมายความว่าเก็บจำนวนคนที่ร่วมวิจัยให้ได้น้อยที่สุด ในขณะเดียวกันก็ต้องให้ข้อมูลอย่างเพียงพอที่สุดที่จะตอบคำถามงานวิจัยได้

การเก็บจำนวนคนให้ได้มากๆ นั้นไม่ใช่ข้อดีเสมอไป นอกจากที่จะเปลืองทรัพยากรที่ใช้ เปลืองแรงคนเก็บ แล้วยังถือว่าเป็นการเปลืองตัวของคนไข้อีกด้วยครับ นั่นคือ เขาไม่จำเป็นจะต้องมาร่วมงานวิจัยก็ได้นั่นเอง (ซึ่งผิดหลักจริยธรรม หรือ Ethics)

ปัญหาของหลายๆ คนคือไม่ทราบว่าจะคำนวณขนาดตรงนี้ยังไงดี ผมขออธิบายง่ายๆ ก่อน ในกรณีของการศึกษาเปรียบเทียบการให้ยา (หรือให้ intervention อื่นก็ได้) สองกลุ่มเปรียบเทียบกันตามแบบ RCT 2 กลุ่มง่ายๆ ยกตัวอย่างเช่น ผมกำลังศึกษาเรื่องการให้ยาต้านไวรัส เทียบกับ placebo ในคนไข้ที่ได้รับการวินิจฉัยว่าเป็นไข้หวัด 2009 แล้วดูว่า อัตราการตาย มันลดลงหรือไม่นะครับ

สิ่งที่เราต้องมีอยู่ในมือมีสามอย่าง และมีในหัวอีกหนึ่งอย่างครับ

• อย่างแรก ต้องมีอัตราการเกิด outcome ในกลุ่ม control นั่นคือ ต้องรู้ว่า คนที่ได้รับ placebo นั้น มีอัตราการตายเป็นเท่าไหร่ อันนี้จะหามาได้จากที่ไหน? เราอาจจะเทียบเคียงมาจากกลุ่มโรคใกล้ๆ กัน, หามาจากการศึกษาแบบ Cross sectional/Cohort หรือหามาจากการทำ Preliminary study (ลองศึกษาในผู้ป่วยจำนวนน้อยๆ 10-20 คน) ก็ได้ครับ



• สิ่งถัดมา คือเราจะต้องรู้ว่าเราอยากจะเทียบให้มันต่างกันสักแค่ไหน ยกตัวอย่างเช่น เรารู้แล้วว่าคนปกติที่ได้ placebo นั้นมีอัตราตาย 1% เราอยากรู้ว่า ถ้าให้ยาต้านแล้วจะช่วยเปลี่ยนอัตรานี้เป็น 0.5% หรือเปล่า ตัวเลขนี้เป็นตัวเลขที่เรากำหนดเอาเองครับ โดยอาจจะเทียบเคียงกันกับความสำคัญทางคลินิก หรือดูจากหลายๆ การศึกษาในโรคอื่นๆ ที่ผ่านๆ มา ถ้าเราตั้งน้อยไป ก็จำเป็นจะต้องใช้ตัวอย่างมาก (เปรียบเหมือน ของที่มีขนาดเล็กๆ ต้องอยู่กันมากๆ ถึงจะเห็น ในขณะที่ของใหญ่ๆ อยู่กันไม่มากก็เห็นแล้ว)



• อย่างสุดท้าย คือการกำหนดค่าทางสถิติที่จะใช้ นั่นคือค่า Alpha และ Beta Error ครับ โดยทั่วไปแล้ว Alpha = 0.05 และ Beta = 0.20



• ส่วนสิ่งที่ต้องมีอยู่ในหัว ก็คือต้องนึกได้ว่าเรากำลังจะวิเคราะห์ข้อมูลแบบใด ซึ่งโดยง่ายๆ แล้วส่วนมากเราจะวิเคราะห์ข้อมูลที่จุดสิ้นสุดของ Trial เป็น Outcome ว่าตาย หรือไม่ตาย ส่วน Exposure เป็นได้ หรือไม่ได้ อันนี้การวิเคราะห์ที่ใช้นั้นใช้วิธีแบบ Pearson Chi-square test (ไว้เรื่องสถิติจะมาเขียนให้ฟังในภายหลังนะครับ)

เราลองมาทำความเข้าใจกับคำว่า Alpha, Beta Error กันนะครับ

เราจะสังเกตได้ว่า มีโอกาสที่ในความเป็นจริง (the truth) -- ในที่นี้คือความเป็นจริงแท้ของตัวโรค -- นั้นการให้ยาสองอย่างมันแตกต่างหรือไม่แตกต่าง และในการศึกษาเรา มันอาจจะแตกต่างหรือไม่แตกต่างกันก็ได้ นั่นหมายความว่า เราทำการศึกษาไปนั้น มีโอกาสที่จะเกิดเหตุการณ์ได้ 4 กรณี

• ในกรณีที่ความเป็นจริงมันแตกต่างกันจริงๆ ส่วนเราศึกษาแล้วก็พบว่าแตกต่างจริงๆ ก็ไม่มีปัญหาอะไร แสดงว่าเราพบถูก (True positive)


• ในกรณีที่ความเป็นจริงมันไม่แตกต่าง และเราศึกษาก็ไม่พบว่ามันแตกต่าง ก้ไม่มีปัญหาเช่นกัน (True negative)


• ในกรณีที่ความเป็นจริงมันไม่แตกต่าง แต่เราดันศึกษาได้ว่ามันแตกต่าง (False Positive)


• สุดท้าย ในกรณีที่ความเป็นจริงมันแตกต่าง แต่เราดันศึกษาแล้วพบไม่แตกต่าง (False Negative)

ปัญหามันอยู่ตรงที่ ถ้าเราสรุปจากการวิจัยได้ไม่ตรงกันกับความเป็นจริงแท้ของตัวโรค มันจะเป็นอย่างไร

• ถ้าความเป็นจริง มันก็ไม่ได้แตกต่างอะไร แต่เราดันไปเจอว่ามันแตกต่างกัน (False Positive) อันนี้เราเรียกว่า Alpha error หรือตำราหลายๆ ที่จะเรียกว่า Type I error ครับ หมายความว่าจริงๆ การให้ยามันไม่ต่างหรอก แต่เราดันไปเจอด้วยโอกาสหรือความผิดพลาดอะไรก็แล้วแต่ แล้วดันสรุปว่าการให้ยามันดีกว่า
  
  ปกติแล้วโอกาสที่จะเกิด Alpha error นี้มักจะำกำหนดให้เป็น 0.05 หรือน้อยกว่า อันนี้ก็คือ Significant level ของเราหรือก็คือที่หลายๆ คนชอบบอกว่า p Value < 0.05 ถือว่า Significant นั่นเองครับ เช่น ผมศึกษาแล้วพบว่าการให้ยานั้นอัตราตายในกลุ่มได้ยา = 0.5% กลุ่มไม่ได้ยา = 1% แล้วพบว่า p Value = 0.05 พอดี นั่นหมายความว่า สิ่งที่ผมพบว่ามันแตกต่างนี้ มีโอกาสที่มันจะเกิดจากความฟลุ๊ค (โดยบังเอิญ) = 0.05 (หรือภาษาชาวบ้านก็คือ 5%)
  
  ทำไมต้องเป็น 0.05 (หรือ 5%) อันนี้ไม่มีใครตอบได้ครับ เพราะจริงๆ แล้วเราจะกำหนดที่เท่าไหร่ก็ได้ จะเอาโหดหน่อย 0.025 ก็ได้ แต่แน่นอนว่าถ้ายิ่งน้อยก็ยิ่งต้องการ Sample size เยอะขึ้นเรื่อยๆ ด้วยครับ



• อันต่อมา ถ้าความเป็นจริงมันแตกต่างกัน แต่เราดันไม่พบความแตกต่างในการทำ Study (False Negative) อันนี้เราเรียกว่า Beta error หรือ Type II error ครับ เช่นยกตัวอย่างเดียวกัน ถ้าผมไม่พบว่ายาต้านไวรัสมันทำให้อัตราตายลดลง แต่ในความจริงแล้วมันดันทำให้ลดลงนั่นเอง
  
  ค่าโอกาสด้านกลับของ Beta (1 - beta) เราจะเรียกว่า Power ของการศึกษานี้ครับ (เหมือนว่าการศึกษาเรามี "พลัง" ในการ detect ความแตกต่างในธรรมชาตินี้ได้ซักเท่าไหร่) โดยทั่วไปเรากำหนด Beta = 0.2 เพราะฉะนั้นแล้วก็มักจะได้ Power = 1-0.2 = 0.8 นั่นเองครับ

เมื่อเรารู้ค่าต่างๆ เหล่านี้แล้วเราสามารถนำมาคำนวณขนาดของตัวอย่างได้ตามสมการสำหรับการคำนวณ n ใน trial ที่ใช้การวิเคราะห์เป็น Chi-square คือ



โดย

P0 = อัตราของ outcome ในกลุ่ม control
P1 = อัตราของ outcome ในกลุ่มที่ให้ intervention นั่นก็คือ อัตรา outcome ของ control - ความแตกต่างที่เราต้องการ detect
P bar = ค่าเฉลี่ยของ P0 และ P1 ก็คือ (P0+P1)/2
Z a/2 = ค่า Z ของ alpha error ในที่นี้ค่า Z a/2 ที่ alpha = 0.05 จะได้ 1.96 (แนะนำว่าของ study ทั่วไปก็เท่านี้ละครับ)
Z b = ค่า Z ของ beta error ในที่นี้ค่า Z b ที่ beta = 0.2 จะได้ 0.84 (แนะนำแบบเดียวกัน)
และ n ที่ได้ออกมานี้ เป็น n ของแต่ละกลุ่ม นะครับ นั่นหมายความว่าเรามีสองกลุ่ม (control/intervention) ก็ต้องคูณ 2 เข้าไปด้วยนะ

ถ้าค่า Z มันเหมือนกันทุกการศึกษา เราก็จะแทนสูตรได้แบบนี้ครับ:



เรามาลองคำนวณดูนะครับ

สมมติว่าผมทำการศึกษาด้วยการให้ยาต้านไวรัสในกลุ่มคนไข้ที่เป็นไข้หวัด 2009 โดยดู outcome คืออัตราการนอนโรงพยาบาล การศึกษาก่อนหน้านี้พบว่าอัตราการนอนโรงพยาบาลในกลุ่มที่ไม่ได้รับยานั้น = 15% และผมอยากรู้ว่าถ้าอัตรามันต่างกัน +- 5% (เป็นเลขสมมติของผมที่ผมคิดว่ามันน่าจะมีความสำคัญนะ ระหว่าง 15 กับ 10%) ที่ Type I error = 5% และ Type II error = 20% นี้ผมต้องใช้ Sample Size เท่าไหร่

เราก็เข้าสูตรมาเลยนะครับ ลองคิดดูกันก่อนนะครับ (ลองแทนก่อนแล้วค่อยดูเฉลยนะครับ)

.
.
.

จากโจทย์ เราจะได้ค่าต่างๆ คือ
P0 = 0.15
P1 = 0.15 - 0.05 = 0.10
Pbar = (P0+P1) /2 = (0.15+0.10) /2 = 0.125
Alpha = 0.05
Beta = 0.20

ดังนั้น เราจะสามารถแทนค่าในสูตรได้ดังนี้



นั่นคือ คำตอบ = 685 คนโดยประมาณในแต่ละกลุ่ม ซึ่งก็คือ คนทั้งหมด = 2*685 = 1370 คนนั่นเอง คิดได้เหมือนกันบ้างไหมครับ?

จริงๆ แล้วเราไม่ต้องมานั่งแทนค่าในสูตรเอาก็ได้ เดี๋ยววันหลังผมจะมาแนะนำวิธีการใช้โปรแกรมช่วยในการคำนวณนะครับ :D

Causality

เคยคิดกันไหมครับ ว่าการที่เราจะบอกว่าอะไรเป็นเหตุเป็นผลกันนั้นมันขึ้นอยู่กับอะไรบ้าง? ลองคิดเอาง่ายๆ ดู สมมุติว่าผมสังเกตเห็นว่าเพื่อนผมหัวล้าน และเห็นเขาชอบกินผงชูรสบ่อย ผมจะบอกได้ไหมว่า การกินผงชูรสบ่อยๆ ทำให้หัวล้าน?

เคยมีคนพิจารณาเรื่องของความเกี่ยวข้องกันนี้แล้วครับ นั่นคือคุณ Hill ซึ่งแกพิจารณาออกมา และมีคนสรุปเป็น Criteria ของการที่เราจะพิจารณาว่าอะไรนั้นเป็นเหตุเป็นผลกันได้ดังนี้ครับ (Bradford-Hill Causal Criteria)

1. Temporality นั้นคือ เหตุ นั้นน่าจะเกิดขึ้นมาก่อนผล ตามตัวอย่างนี้ก็คือ เขาควรจะกินผงชูรส ก่อนที่จะหัวล้าน ไม่ใช่ หัวล้านเกิดก่อน แล้วค่อยกินผงชูรส


2. Strength ของความสัมพันธ์ เหตุเล็กๆ ที่ทำให้เกิดผลใหญ่ๆ มาก (ทางสถิติก็คือมี Odds Ratio/Relative Risk สูงๆ) ก็น่าจะเป็นเหตุเป็นผลกัน (ข้อนี้ระวังนิดนึง ตรงที่ผลที่มันเจอบ่อยๆ อาจทำให้สับสน นอกจากนี้เหตุที่ไม่ได้เป็นต้นเหตุจริงๆ แต่ดันสัมพันธ์กับต้นเหตุอื่นๆ เช่น ผู้ชาย --> เป็นมะเร็ง แต่จริงๆ แล้ว ผู้ชาย --> ชอบสูบบุหรี่ --> เป็นมะเร็ง อันนี้ก็อาจจะบอกลำบากว่าการเป็นผู้ชายทำให้เกิดผลเป็นมะเร็ง)


3. Dose-response คือการที่ถ้ามีต้นเหตุขนาดใหญ่ขึ้น จะทำให้ผลลัพธ์ขนาดใหญ่ขึ้นไปด้วย เช่น ยิ่งกินผงชูรสปริมาณมากขึ้น ยิ่งหัวล้านขึ้น


4. Consistency คือคนอื่นทดลองค้นคว้าแบบเดียวกัน ก็ได้ผลลัพธ์คล้ายๆ กัน


5. Biologic Plausibility คือมีคำอธิบายทางวิทยาศาสตร์ที่ดูแล้วน่าจะเป็นไปได้ เช่น กินผงชูรส ทำให้โซเดียมในร่างกายเยอะขึ้น มีผลต่อระบบฮอร์โมน และทำให้ผมร่วงมากขึ้น จนเกิดหัวล้าน (อันนี้อย่าเชื่อนะครับผมสมมติเฉยๆ)


6. Reversibility คือถ้าเอาเหตุออก ผลก็ควรหายออกไปด้วย


7. Specificity คือความสัมพันธ์นั้นๆ ทำให้เกิดผลลัพธ์เพียงอย่างเดียว เช่น กินผงชูรส ก็เกิดแต่ผมร่วง ไม่เกิดอาการสีผิวเปลี่ยนเป็นต้น


8. Analogy คือดูแล้วมันคล้ายๆ กับ Factor อื่นๆ อันนี้ลองยกตัวอย่างเช่น การสูบบุหรี่ทำให้เกิดมะเร็งปอด ดังนั้นถ้าเราศึกษาการสูบใบจาก (ที่ไม่ใช่บุหรี่ แต่คล้ายๆ กัน) แล้วพบว่าเกิดมะเร็งปอด ก็น่าจะคิดได้ไปในทางเดียวกัน เพราะคล้ายๆ กับบุหรี่


9.  Experimental evidence เป็นข้อที่สำคัญที่สุด เนื่องจากว่าหากมีการศึกษาแบบทดลองให้เหตุแล้ว ดันมีผลเกิดขึ้นนั้นก็เป็นสิ่งที่น่าจะยืนยันได้ว่า มันน่าจะเป็นเหตุเป็นผลกันจริงๆ

สำหรับความสัมพันธ์อันไหน ที่ยิ่งมี Causal Criteria เยอะๆ นั่นก็หมายความว่ามันน่าจะเป็นเหตุเป็นผลกันมากขึ้นเรื่อยๆ ครับ บางคนก็อาจให้น้ำหนักของแต่ละข้อไม่เท่ากันก็ได้ อันนี้ก็แล้วแต่จะพิจารณา

ลองมาคิดกันดูนะครับว่า Analytic Study Design แบบไหนที่จะตอบ Causality ได้ดีมากที่สุด และดีรองลงมาๆ (ใครจำว่า Study Design มีอะไรบ้างไม่ได้ กรุณาอ่านเอนทรี่เก่าเรื่อง Study Design ที่ผมเคยเขียนไว้โดยด่วน)

.

.

.

สังเกตว่า Study รูปแบบที่จะตอบคำถามเหตุผลนี้ดีที่สุด ก็ควรจะเป็น Experimental Study ครับ ส่วน Observational Study ที่จะช่วยได้บ้างก็คือ แบบ Cohort เนื่องจากมี Temporal relationship (เราศึกษาจากเหตุไปยังผล) ส่วน Case-control นั้นก็รองลงมา และที่แย่ที่สุดคือการศึกษาแบบ Cross-sectional ครับ :D

สำหรับใครที่อยากอ่านเพิ่มเติมเรื่องนี้ ผมแนะนำให้อ่าน Paper ของ Rothman: Rothman KJ, Greenland S. Causation and Causal Inference in Epidemiology. Am J Public Health. 2005 Jul 1;95(S1):S144-150. ครับ

Regression towards the mean

ก่อนจะกลายเป็นบล็อกร้าง ต้องขออภัยทุกท่านที่หายไปพอสมควรนะครับ พอดีตอนนี้ผมเรียนอยู่ตลอดเลย วันนี้ขอเรื่องสั้นๆ คือ "Regression towards the mean" ครับ

คำนี้ได้ยินครั้งแรกๆ ก็อาจจะงงกันนะครับ ว่ามันเป็นอย่างไร เรื่องของเรื่องนั้นมาจากท่าน Sir Francis Galton ซึ่งเป็นนักพันธุศาสตร์ในช่วงปี 1900 แกสังเกตว่า สิ่งที่มันประหลาดเอามากๆ เช่น การที่มีความสูงเกินกว่าคนปกตินั้น ไม่ได้ถ่ายทอดทางพันธุกรรมจากพ่อไปสู่ลูกเท่าไหร่ และแกเห็นว่าพ่อที่ตัวสูงเกินเหตุนี้แทบจะมีลูกที่ตัวเตี้ย เข้าใกล้ค่าเฉลี่ยของคนปกติอยู่เสมอ แกก็เลยสรุปว่ามันน่าจะเป็นปรากฎการณ์อะไรซักอย่าง

จริงๆ แล้วสิ่งที่เราเห็นอยู่นี้ไม่ใช่ปรากฎการณ์แปลกประหลาดอะไร มันเป็นสิ่งที่เราเข้าใจได้ตามธรรมชาติอยู่แล้วครับ เช่นผมเปิดร้านขายไอศครีมอยู่ มีลูกค้าโดยเฉลี่ยทั้งปีที่ผ่านมาประมาณ 100 คนต่อวัน ปรากฎว่าวันดีคืนดีผมเปิดร้านมามีลูกค้า 1,000 คนมารออยู่หน้าร้านโดยไม่มีเหตุอะไรเกิดขึ้น ทุกคนก็คงคิดได้ใช้ไหมครับว่ามันเกิดจากความ "ฟลุ๊ก" และวันต่อไปนั้น "ลูกค้าก็คงจะลดกลับมาเท่ากับค่าเฉลี่ยเหมือนเดิม" ตรงนี้แหละครับคือ Regression towards the mean

ในทางเดียวกันค่าที่มัน "เกินเหตุ" (Extreme) นี้ไม่จำเป็นจะต้องเป็นค่าที่สูงไปอย่างเดียว ค่าที่ต่ำไปก็มีแนวโน้มที่จะกลับมาสู่ Mean เหมือนกัน เช่นวันดีคืนดีผมดันไม่มีลูกค้ามาซื้อไอศครีมเลย ก็คงคิดได้ว่าวันต่อไป "ลูกค้าก็คงจะเพิ่มกลับเข้าใกล้ 100 คนเหมือนเดิม" เช่นเดียวกันครับ

ถามว่ามันเกี่ยวข้องอะไรกับระบาดวิทยา? มันเกี่ยวข้องในแง่ของ "การวัด" ครับ นั่นหมายความว่า ในคนที่เราเจอค่าอะไรที่ผิดปกติมากๆ ในครั้งแรกนั้น เราก็มีโอกาสเจอค่าที่มันเข้าใกล้ปกติมากขึ้นในครั้งต่อไป เช่น ถ้าพบว่าเจาะเลือดดูน้ำตาล (เบาหวาน) ในเลือดในครั้งแรกดันได้ทะลุเป้า ครั้งต่อมานั้นถึงแม้ว่าจะให้หรือไม่ให้ยาอะไร มันก็ "น่าจะ" มีแนวโน้มในการเข้าใกล้ค่า mean ของคนๆ เดิมเหมือนเดิมครับ

นั่นเป็นสาเหตุที่เราจำเป็นจะต้องมีกลุ่มควบคุม (Congrol Group) ในการศึกษาครับ เพื่อป้องกัน Bias จาก Regression towards the mean นี่เอง! (ดังนั้นแทบจะสังเกตได้ง่ายๆ ว่า อะไรที่วัดก่อนและหลัง โดยไม่มีกลุ่มเปรียบเทียบ มันมักจะดีขึ้นอยู่เสมอๆ)

Systematic Review & Meta-analysis

จากที่ผมเคยสัญญาว่าจะเขียนเรื่องเกี่ยวกับการ Appraise Systematic Review นะครับ ก่อนอื่นเลยก็ต้องขอพูดเกริ่นนำเรื่อง Systematic Review และ Meta-analysis ก่อนครับ

Systematic Review โดยนิยามนั้นหมายถึงการรวบรวมคำตอบของคำถามที่จำเพาะเจาะจงครับ ลองนึกสภาพถึงคำถามที่เกิดขึ้นในทางคลินิกนะครับ คำถามในที่นี้ก็จะล้อกันไปกับ PICO นั่นละครับ ตัวอย่างเช่น

• การให้ Aspirin ในผู้ป่วยเบาหวานช่วยลดการเกิด MI หรือไม่
• การให้ แป๊ะก๊วย ช่วยลดอาการปวดขาเป็นพักๆ (intermittent claudication) หรือไม่
• การผ่าตัดถุงน้ำดีแบบส่องกล้อง (laparoscopic cholecystectomy) ลดอัตรา complication หรือไม่เมื่อเทียบกับการผ่าแบบเปิด (open cholecystectomy)
• ฯลฯ

เมื่อมีการตอบคำถามเหล่านี้มากขึ้นเรื่อยๆ ไม่ว่าจะเป็นจากทั้งการศึกษาแบบ observational (cohort/cross-sectional) หรือ experimental (RCT) มันก็คงไม่สะดวกเวลาตอบใช่ไหมครับ หากเราต้องมานั่งอ่านเป็นสิบเปเปอร์ มันจะดีกว่ามั้ยถ้าเรารวมคำตอบไว้ทีเดียวเลย นั่นคือที่มาของ “review” ครับ

แต่หลายๆ ท่านก็คงเคยอ่าน review โดยทั่วๆ ไปแล้วนะครับ เช่นจากพวก textbook หรือ article review ที่อ่านตามหนังสือทั่วไป ปัญหาของพวก review พวกนี้ที่เกิดขึ้นก็คือว่า มัน “ไม่เป็นระบบ” ครับ คนทำอาจจะเอนเอียงไปข้างใดข้างหนึ่งก็ได้ (เช่นคนเขียนนั่งอยู่ที่บริษัทเครื่องมือผ่าตัดส่องกล้อง เขียนเชียร์ตัวเองอยู่) ทำให้ผลที่ได้อาจจะไม่ได้พูดถึงในอีกแง่มุมหนึ่งเลย จุดนี้เอง เป็นที่มาของการทำ Systematic Review ครับ

ขั้นตอนของการทำ Systematic Review ขั้นแรกก็คือการตั้งปัญหาที่เราสนใจครับ ปัญหานั้นจะต้องค่อนข้างเจาะจง เพื่อที่เราจะได้ตอบได้ครับ หลังจากนั้นเราจะต้องหาคำตอบของปัญหานี้ด้วยวิธีที่เป็นระบบ โดยอาจจะมีการตั้งกฎเกณฑ์ที่เป็นระบบไว้ก่อน เช่น ตั้งว่าจะค้นหาด้วยวิธีใดบ้าง ค้นฐานข้อมูลใด ใครค้น คัดเลือกด้วยใคร ใครเป็นคนกรอกข้อมูล ข้อมูลที่ได้จะรวมกันแบบไหน อย่างใด เสมือนหนึ่งเดียวกับการทำวิจัยชนิดอื่นๆ เลยครับ (นั่นจึงเป็นที่มาของคำว่า “Systematic”)

ขั้นต่อมาก็คือการค้นคว้าครับ ในขั้นตอนการค้นคว้านี้ ฐานข้อมูลที่เป็นที่นิยมโดยส่วนมากก็คือ Medline ครับ ไม่ต้องงงนะครับ จริงๆ ก็คือฐานข้อมูลที่ PubMed มีอยู่นั่นละครับ (PubMed เป็นชื่อของ “ตัวค้น” – Search Engine ส่วน Medline เป็นชื่อของ “ฐานข้อมูล” – Database) ส่วนฐานข้อมูลอื่นๆ ที่นิยมก็เช่น EMBASE (ของฝั่งยุโรป), CINAHL, Cochrane Controlled Trial Register เป็นต้นครับ นอกจากนี้ยังอาจจะค้นจากสื่ออื่นๆ เช่น ค้นจากการติดต่อ Expert, ค้นจากรายงานของ Conference ต่างๆ ด้วยก็จะยิ่งดีครับ

หลังจากที่เราค้นหาหลักฐานต่างๆ จากฐานข้อมูลนี้มาได้แล้ว เราก็จะต้องมาดูว่าเปเปอร์ไหนบ้างที่เข้ากับคำถามของเราครับ (ตรงจุดนี้จะต้องมีกำหนดไว้ก่อนในช่วงแรกแล้วอย่างแน่ชัดเป็น inclusion/exclusion criteria มิเช่นนั้นจะกลายเป็นว่าเรา “เลือก” หลักฐานมา – เป็น selection bias นั่นเองครับ)

เมื่อได้เปเปอร์มาแล้ว ผู้วิจัยส่วนใหญ่ก็จะให้คะแนนความน่าเชื่อถือของเปเปอร์ครับ โดยคะแนนความน่าเชื่อถือนี้มีหลายแบบครับตามแต่ว่าเปเปอร์ที่เลือกมานั้นเป็นประเภทใด เช่นถ้าเป็นของ RCT ก็จะเป็น JADAD score เป็นต้นครับ

หลังจากนั้นผู้วิจัยก็อาจจะสรุปเลยก็ได้ครับว่าหลังจากที่ค้นมาแล้วเป็นอย่างไรบ้าง แต่ส่วนใหญ่มักจะไม่จบเพียงแค่นี้ครับ (เพราะเสียดายอุตส่าห์ค้นมาตั้งเยอะ) ส่วนใหญ่เขาก็จะดึงเอาข้อมูลออกมา เพื่อที่จะนำข้อมูลนั้นมารวมกันด้วยวิธีการทางสถิติ ที่เรียกกันว่า meta-analysis กันนั่นเองครับ (โดยอาจจะมี Forest Plot + Heterogeneity Test ตามที่เคยเขียนไปแล้วด้วยครับ) นอกจากนี้ยังอาจจะวิเคราะห์ย่อยๆ ด้วยเช่นว่า ถ้าแบ่งเปเปอร์เป็นกลุ่มๆ แล้วจะมีคำตอบแตกต่างกันไปหรือไม่ เช่นผมรวม RCT ที่เกี่ยวกับการให้ Aspirin ในคนไข้เบาหวาน แต่มันมีทั้งเบาหวานแบบที่มีความดันร่วมด้วย หรือไม่มีความดันร่วมด้วย ผมอาจจะแบ่งข้อมูลเป็นสองกลุ่ม แล้วดูว่ามันต่างกันหรือไม่ก็ได้ครับ ซึ่งเรียกว่าการทำ Subgroup analysis

นอกจากการนำข้อมูลของเปเปอร์อื่นมารวบรวมด้วยกันแล้ว เรายังอาจจะนำเอาข้อมูลของ “คนไข้” ในแต่ละเปเปอร์นี้มารวมกันได้ด้วยครับ นั่นก็คล้ายกับว่าผู้วิจัยเสมือนหนึ่งเป็นการรวม Trials ต่างๆ เข้าด้วยกัน ซึ่งทำให้จำนวน n มากขึ้นนั่นเองครับ การนำข้อมูลคนไข้มารวมกันนี้ บางทีก็จะเรียกว่าเป็น Individual Patient Data ครับ

และสุดท้ายที่ผู้วิจัยอาจจะนำเสนอก็คือการแสดง Publication Bias ครับ Publication Bias ก็คือการที่ Study ที่ไม่ได้ผลนั้นอาจจะไม่ได้ลงตีพิมพ์ในฐานข้อมูล ทำให้เราอาจจะ “หลุด”  Study ที่ไม่ได้ผลก็ได้ครับ เช่น RCT ที่ให้แป๊ะก๊วยแล้วไม่ได้ผล ก็อาจจะไม่มีสำนักพิมพ์ไหนอยากเอาไปพิมพ์ ทำให้ในฐานข้อมูลทั้งหมดกลายเป็นมีแต่แป๊ะก๊วยใช้ได้ผล ทั้งๆ ที่มันก็มี RCT ที่ให้แล้วไม่ได้ผลเหมือนกัน ตรงจุดนี้เราสามารถพล็อตกราฟเพื่อดูได้ครับว่า ผลมันไปทางเดียวกันหมดเลยหรือเปล่า (กราฟที่นิยมคือ Funnel Plot ครับ)

กล่าวโดยสรุปแล้ว ถ้ามีการวางแผนและทำเป็นระบบนั้น ก็จะยิ่งเพิ่มความน่าเชื่อถือของการทำ Systematic Review เข้าไปอีกครับ นั่นเองเป็นที่มาของว่า ทำไม Systematic Review นั้นถึงได้อยู่ในอันดับต้นๆ ของ Hierachy of evidence ครับ

ติดตั้งแพคเกจใน R ผ่าน Proxy/ติดตั้งด้วยมือ

เคยมีคนถามผมครับว่าโปรแกรม R นั้นจะลงแพคเกจเสริมได้อย่างไร หากว่าเราต้องต่ออินเทอร์เน็ตผ่าน Proxy หรือเราดาวน์โหลดแพคเกจนั้นมาลงเอง

วิธีการก็ไม่ได้ลำบากอะไรเท่าไหร่ครับ แทนที่เราจะเริ่มโปรแกรม R ขึ้นมาเอง ให้คลิ๊กขวาในไอคอนของโปรแกรมใน Start Menu แล้วเลือก Properties



หลังจากนั้นพิมพ์เพิ่มเติมในช่อง Target จากเดิมที่เป็น:

"C:\Program Files\R\R-2.9.0\bin\Rgui.exe"

ให้ต่อท้ายด้วยเว็บ proxy แบบนี้แทน:

"C:\Program Files\R\R-2.9.0\bin\Rgui.exe" http_proxy=<ชื่อ proxy> http_proxy_user=ask

เช่นอย่างของมหิดล proxy นั้นคือ proxy-phy1.mahidol:8080 ก็จะเป็นแบบนี้ครับ:

"C:\Program Files\R\R-2.9.0\bin\Rgui.exe" http_proxy=proxy-phy1.mahidol:8080 http_proxy_user=ask

คราวนี้เวลากดเลือก Install Package ก็จะมีหน้าขึ้นมาให้ใส่ชื่อผู้ใช้และรหัสผ่านเหมือนโปรแกรมอื่นๆ แล้วครับ



สำหรับท่านที่ดาวน์โหลดแพคเกจมาเองจาก CRAN ให้เลือกเป็น Windows binary แล้วเลือกเมนู Packages -> Install package(s) from local zip files ครับ



อ้อ ตอนนี้ R มีถึงเวอร์ชัน 2.9.0 แล้วนะครับใครยังไม่ได้อัพเดตก็อัพเดตได้แล้วครับ

Forest Plots and Heterogeneity Tests in Meta-analysis

ครับ วันนี้ผมขอเขียนถึงเรื่อง Forest Plot และ Heterogeneity Test ใน Meta-analysis นะครับ เพราะมีคนถามถึงบ่อย

Forest Plot นั้นก็คือการเรียบเรียงรายละเอียดของแต่ละ Study ย่อยครับ ปกติแล้วเวลาเอา RCT มาสรุปด้วยวิธีการทางสถิตินั้นมันจะมีแต่ตัวเลขเต็มไปหมด เขาก็เลยอาศัยกราฟขึ้นมาเพื่อให้เราสามารถตีความผลลัพธ์ที่ได้ดีขึ้นครับ

ยกตัวอย่างนะครับ จาก Systematic Review เรื่องการรักษาหูหนวกแบบฉับพลันที่ลงใน Arch Otol Laryngol: Conlin AE, Parnes LS. Treatment of sudden sensorineural hearing loss: II. A Meta-analysis. Arch Otolaryngol Head Neck Surg. 2007 Jun ;133(6):582-6. เขาทำการศึกษารวบรวม RCT ที่ให้ Steroid ในคนไข้หูหนวกฉับพลัน เทียบกับคนที่ได้ Placebo และ Outcome เป็นการหายจากหูหนวก โดยพบว่ามี 2 Study ย่อยดังนี้ครับ (คลิ๊กเพื่อดูรูปใหญ่นะครับ):

สังเกตนะครับ ว่าเขาจะเอาแต่ละ Study มาเรียงกันเป็นบรรทัด แล้วก็พล็อตเป็นเส้นขีด รวมถึงมีจุดสี่เหลี่ยมอยู่ตรงกลาง หลังจากนั้นเขาจะแสดงบรรทัด Total (คือการรวมของทุก Study) แล้วแสดงด้วยสี่เหลี่ยมข้าวหลามตัดไว้ในกราฟครับ สังเกตว่าถ้าเราตะแคงหัว 90 องศาจะเห็นกราฟนี้เป็นคล้ายๆ ป่าของต้นไม้ (นั่นคือที่มาของชื่อ Forest Plot น่ะเอง)

วิธีอ่านก็ไม่ยากเย็นอะไรครับ เช่นของ Study แรกนั้นก็แสดง OR อยู่ที่จุด 3.22 (จุดสี่เหลี่ยมจะอยู่ที่ 3.22) และมี 95% CI อยู่ที่ 1.18-8.76 (เส้นขีดจะขีดตั้งแต่ 1.18 ถึง 8.76) วิธีแปลผลก็แปลแบบ OR ธรรมดา (ลองอ่านโพสต์เก่า) เช่นในที่นี้ก็คือ คนที่ได้สเตียรอยด์ มีโอกาสหายเป็น 3.22 เท่าเมื่อเทียบกับ Placebo โดยเรามีความมั่นใจว่า ถ้าทำการทดลอง 100 ครั้งนั้น 95 ครั้งค่านี้จะอยู่ระหว่าง 1.18 ถึง 8.76 เท่าครับ (หรืออีกอย่างคือ ค่านี้มันน่าจะอยู่ในระหว่าง 1.18-8.76)

ส่วน Study อันที่สองนั้นก็เหมือนกันครับ ลองแปลดูเองก่อนนะครับ

.

.

นั่นคือ คนที่ได้ Steroid มีโอกาสหายเป็น 0.89 เท่าเมื่อเทียบกับคนที่ได้ Placebo โดยเรามั่นใจว่ามันจะอยู่ระหว่าง 0.10-7.86 ถ้างงว่าควรแปลยังไง เอาอะไรเทียบอะไร ให้เหลือบไปมองใต้กราฟครับ ว่าของเรามันอยู่ในช่วงที่ Favor Steroid หรือ Favor Placebo

ทีนี้ก็มาถึงตรงสรุปแล้วครับ ก็แปลแบบเดียวกันเป๊ะเลย แต่กราฟเขาพล็อตไว้ให้รูปมันแตกต่างไว้นั่นเอง จากกราฟนี้เราจะสรุปว่า คนที่ได้ Steroid นั้นจะมีโอกาสหายเป็น 2.47 เท่าของคนที่ได้ Placebo โดยเรามั่นใจว่ามันจะอยู่ที่ 0.89 ถึง 6.84 เท่านั่นเองครับ

สำหรับว่าทำไมสี่เหลี่ยมของสอง Study มันถึงขนาดไม่เท่ากัน นั้นถ้าอธิบายง่ายๆ ก็คือมันมีจำนวนคนใน Study นั้นไม่เท่ากันครับ เพราะฉะนั้น Study ที่คนน้อยกว่า เขาก็จะให้น้ำหนักน้อยกว่า (จริงๆ แล้วมีหลายวิธีในการให้น้ำหนักใน Study แต่ที่ง่ายๆ ก็คือให้ตามปริมาณคนใน Study)

ทีนี้ก็มาถึงการแปลผลของ Heterogeneity แล้วครับ

Heterogeneity คืออะไร? Heterogeneity แปลว่า ความไม่เป็นเนื้อเดียวกันครับ ง่ายๆ เลยคือเหมือนเราเอา ส้มเขียวหวาน มารวมกับ มะนาว แล้วดูเรื่องความเปรี้ยว แล้วเราจะเอามาสรุปว่าส้มมันเปรี้ยวก็คงลำบาก เนื่องจากว่าก็รู้ๆ อยู่ว่ามะนาว มันไม่ใช่ส้ม นั่นคือมันไม่เป็นเนื้อเดียวกัน หรือเป็น Heterogeneity นั่นเองครับ

ทีนี้เราจะบอกได้ยังไงว่าสิ่งที่เราดูอยู่มันต่างกัน? เพราะมันไม่ได้ง่ายเหมือนส้มหรือมะนาว… วิธีการของนักสถิติคือ เขาจะดูว่าค่าที่ได้มันไปในอารมณ์เดียวกันหรือเปล่าครับ โดยวิธีดูด้วยตาเปล่าคือ กราฟ 95%CI มันคร่อมกันหรือเปล่านั่นเอง

แต่ทั้งนี้เนื่องจากว่าเป็นนักสถิติ จะอธิบายด้วยตาเปล่าคงยังไงๆ อยู่ เขาก็เลยใช้วิธีการทางตัวเลขมาเพื่อตอบปัญหาในกรณีนี้ นั่นคือ Heterogeneity Test นั่นเองครับ โดย Heterogeneity Test นั้นมีสมมติฐานหลักว่า แต่ละค่าของการศึกษานั้นเป็นไปในทางเดียวกัน แล้วพยายามหาค่าโอกาสของความที่ Study มันต่างกัน (ซึ่งเป็น p-Value ของ Test) มาหักล้างนั่นเอง

อย่างในตัวอย่างข้างต้นที่กล่าวไป นั่นคือเขาทำ Heterogeneity Test ได้ Chi2 = 1.11 เมื่อแปลงมาเป็นค่า p-Value แล้วได้ 0.29 นั่นหมายความว่า “ในทางสถิติแล้ว โอกาสที่จะมี Study ที่ต่างกันซ่อนอยู่ (โอกาสที่มีมะนาวแอบอยู่) นั้น = 29%”

แล้วเราจะเอาเท่าไหร่เป็น cut-point ว่ามันเหมือนหรือไม่เหมือนละ? อันนี้ไม่มีคำตอบครับ ส่วนใหญ่เนื่องจาก Test นี้มันโหดน้อยไปหน่อย ถ้าเอา 0.05 แบบการแปลผล p-Value ทั่วไปแล้ว ก็จะกลายเป็นว่าทุกอันแทบไม่มีอันไหนไม่ต่างกันเลย เขาจึงเอาที่ 0.10 เป็นเกณฑ์ครับ หมายความว่า Study ใดๆ ที่มันได้ p น้อยกว่า 0.10 นั้นมันอาจมีความแตกต่างกันของ Study ซ่อนอยู่ภายใน

หรือถ้าในกรณีนี้ p=0.29 ก็คือ Study มันน่าจะไปในทางเดียวกันนั่นเอง ซึ่งสอดคล้องกับการที่ 95%CI มันคร่อมกันอยู่

ต่อจากนี้แล้วช่วงหลังเขาจะนิยมใส่ค่า I2 เข้ามาด้วยครับ ค่านี้เป็นค่าที่ได้มาจากการคำนวณของ Heterogeneity อีกทีหนึ่ง ซึ่งจะดีกว่าตรงที่มันไม่ต้องมี Cutpoint มันจะบอกเป็น % ให้เลยว่าโอกาสที่ Study มันแตกต่างน่าจะซักเท่าไหร่

อย่างในกรณีนี้ I2 = 9.5% แสดงว่ามันค่อนข้างไม่แตกต่างเท่าไหร่ครับ.. เอ แล้วจะเอาเท่าไหร่มาบอกว่ามันแตกต่างกันเยอะมากน้อยละ? อันนี้ก็กลับมาเรื่อง cutpoint อีกเหมือนเดิม แต่มีคนแนะนำคร่าวๆ ไว้ถ้าเกิดว่ามัน <25% มันก็แตกต่างไม่เท่าไหร่ 25-50% แตกต่างมากหน่อย >50% ควรระวังได้แล้ว แต่ทั้งนี้อย่าลืมว่า cutpoint นั้นไม่ใช่จุดชี้ชะตานะครับ เป็นแค่คำแนะนำจากนักสถิติเท่านั้นเอง (เพราะงั้นหนังสือแต่ละเล่มย่อมไม่เหมือนกันแน่ๆ)

แล้วทีนี้ Study แต่ละอันจะแตกต่างกันได้ยังไงบ้าง Source ของ Heterogeneity มันจะมาจากไหน?

• อาจแตกต่างกันในแง่ของการดำเนินงาน เช่น ทำในประชากรคนละที่, ให้ยาคนละ dose, เก็บข้อมูลกันคนละแบบ
• หรือแตกต่างในแง่ของคุณภาพการศึกษา (methodology quality) เช่น Randomize ดี รัดกุม อีกอัน โยนหัวก้อย หรืออันหนึ่ง Blind อีกอันไม่ Blind เป็นต้น

ซึ่งบางครั้งใน Meta-analysis ก็อาจแบ่ง Study เป็นหลายๆ แบบเพื่อดูว่าถ้าแบ่งตามยา dose น้อยแล้วผลมันจะเป็นอย่างไร หรือถ้าเอาเฉพาะ Study ที่คุณภาพดีๆ นั้นจะไปทางเดียวกันหรือเปล่า (ซึ่งก็อาจใช้ค่า I2 มาดูนั่นแหละครับว่าแบ่งแล้วมันดีขึ้น หรือมันแย่ลง)

สำหรับ Test for Overall Effect นั้นเป็นเรื่องเกี่ยวกับ Random Effects และ Fixed Effect Model ซึ่งค่อนข้างจะอธิบายนานครับ ยังไงผมขอผ่านไปก่อน เดี๋ยววันหลังจะมาอธิบายในตอนการ Appraise Systematic Review อีกทีให้นะครับ :)

Hierarchy of evidence

วันนี้ขอพูดถึงเรื่อง ลำดับความสำคัญของหลักฐานนะครับ

ทำไมเราถึงต้องมานั่งจัดลำดับความสำคัญของหลักฐาน (Hierarchy) ? นั่นก็เพราะมันมี “ความน่าเชื่อถือ” ของหลักฐานนั้นไม่เท่ากันครับ ยกตัวอย่างใกล้ตัวเช่น ข่าวลือในอินเทอร์เน็ต หรือ Forwarded mail ว่าดาราคนนั้นกำลังระหองระแหงกับดาราอีกคน เราก็คงคิดว่า อูย มันไม่รู้ว่าจะเชื่อได้หรือเปล่า บางคนก็เชื่อ บางคนก็ไม่เชื่อ แต่ในขณะเดียวกัน ถ้าเกิดว่าดาราคนนั้นเขาออกมาให้สัมภาษณ์ผ่านโทรทัศน์ ก็รับรองว่าทุกคนจะต้องเชื่อแน่นอน (ยกเว้นบางคนที่ขี้ระแวง) นั่นก็หมายความว่า ข่าวลือในอินเทอร์เน็ตนั้นมัน “น่าเชื่อถือ” น้อยกว่าข่าวจากปากเจ้าตัวนั่นเองครับ

ในทางเดียวกัน ความน่าเชื่อถือในการศึกษาต่างๆ นั้นก็มีไม่เท่ากัน โดยทั่วไปแล้วมีคนเสนอหลักคร่าวๆ คือ

• ถ้าดูตาม Design: Experimental Design (ที่คนศึกษาสามารถกำหนดปัจจัยต่างๆ เอง) นั้นน่าเชื่อถือกว่า Observational Design แล้วถ้าเป็น Observational Design ที่ n (ปริมาณคนใน study) มาก ย่อมน่าเชื่อถือกว่า n น้อยๆ
• Prospective มักจะน่าเชื่อถือว่า Retrospective (เรากำหนดสิ่งต่างๆ ที่จะวัด แล้วค่อยมาวัด ย่อมดีกว่า ได้ข้อมูลครบถ้วนกว่า)
• ถ้าดูตามจำนวน Study: ถ้ามีหลาย Study ย่อมดีกว่ามี Study เดียว (ทำนองว่าหลายหัวดีกว่าหัวเดียวงั้นเหอะ)

เมื่อนำหลักพวกนี้มาพิจารณาแล้วจะพบว่า Study ทั้งหลายแหล่ที่เราพบกันบ่อยๆ นั้นควรจะมีลำดับขั้นความน่าเชื่อถือดังนี้

• Systematic Review/Meta-analysis of Randomized Controlled Trial (RCT) น่าเชื่อสุด
• RCT ใหญ่ๆ
• RCT เล็กๆ (หรือ RCT ที่ออกแบบได้ไม่ดี)
• Controlled Trial อื่นๆ ที่ไม่ได้ Randomized
• Systematic Review of Observational Study
• Cohort Study
• Case-control Study
• Case series
• Case report
• Concensus conference
• Expert opinion น่าเชื่อน้อยที่สุด

อย่างไรก็ดีลำดับความน่าเชื่อถือนี้มีผู้โต้แย้งมากมาย บางคนอาจจะสลับกันว่า Controlled Trial เอาไว้ล่างกว่านี้ หรือ Concensus ไว้ข้างบนหน่อย สำหรับผมแล้ว ผมคิดว่าลำดับตามนี้ก็ค่อนข้างมีเหตุผลครับ เช่น Case Series > Case Studies นั้นเพราะมีตัวอย่างคนไข้เยอะกว่า สำหรับ Concensus conference ย่อมมีหลายหัวมากกว่า Expert หัวสองหัว Systematic Review ย่อมดีกว่า Study แต่ละอันเนื่องจากข้อมูลเยอะกว่า

ดังนั้นเวลาที่เราจะพยายามตอบคำถามต่างๆ เราก็ควรที่จะยึดหลักตามนี้ด้วยครับ ถ้ามันมีข้อมูลที่น่าเชื่อถือตามลำดับสูงกว่า เราก็น่าจะเลือกอันนั้นมาตอบคำถามของเรา (แต่อย่าลืมว่าข้อมูลนั้นจะต้องคล้ายคลึงกับคนไข้เราด้วยนะครับ) ยกเว้นเพียงอย่างเดียว คือ โดน expert บีบคอให้เชื่อ :P

และลำดับความสำคัญนี้เองครับ เป็นที่มาของ Grading of Recommendation ตามที่เราเห็นใน Guideline ต่างๆ ครับ เช่นว่า Level A recommendation, Level B recommendation (ระบบ Grading นี่มีหลายระบบมาก และแต่ละระบบก็แบ่งไม่เหมือนกัน ต้องลองดูในเอกสารประกอบ Guideline จะมีระบุไว้ครับ ว่าเขาหมายถึง Study Design แบบใดบ้างครับ)

ถ้าสนใจเรื่องนี้ลองอ่านเพิ่มเติมได้ที่ University of Westminster นะครับ

ย้ายเว็บไซต์

เพื่อเป็นการสะดวกสำหรับทุกท่านที่ต้องการเยี่ยมชมเว็บไซต์ ตอนนี้ผมได้จดทะเบียนชื่อโดเมนในอินเทอร์เน็ตใหม่นะครับ
ท่านสามารถเข้าบล็อกผมได้ผ่านทาง http://www.clinicalepi.com ครับ (จำง่ายดีมั้ยครับ ;) ) ทุกท่านสามารถเข้าทางเดิมก็ได้ หรือทางที่อยู่ใหม่ก็ได้ครับ

เขียน Reference ด้วย Zotero

การเขียน Reference นั้นเป็นเรื่องที่หลีกเลี่ยงไม่ได้สำหรับการเขียนเอกสารทางวิชาการในปัจจุบันครับ เนื่องจากถ้าเราไม่มีที่มาอ้างอิงแล้ว ข้อมูลที่เรายกขึ้นมาลอยๆ นั้นอาจจะดูไม่น่าเชื่อถือ นอกจากนี้ยังไม่ให้ความเคารพแก่เจ้าของความคิดเดิมด้วยในบางกรณี แต่หลายท่านคงจะเบื่อที่จะต้องมานั่งเขียนที่มาเองเหมือนเด็กมัธยม วันนี้ผมขอเสนอวิธีช่วยงานด้วยโปรแกรม Zotero ครับ

โปรแกรม Zotero (อ่านว่า zoh-TAIR-oh) นั้นถูกพัฒนาขึ้นด้วยความสนับสนุนจาก George Mason University ครับ โดยก่อนหน้าที่จะมีโปรแกรมนี้ขึ้นมานั้น ผู้คนส่วนใหญ่มักใช้โปรแกรมอื่น เช่น EndNote (เดี๋ยวนี้ก็ยังใช้กันอยู่) แต่ปัญหามันมีอยู่ว่าโปรแกรมพวกนี้มันไม่ฟรี ต้องเสียเงิน นอกจากนี้ยังใช้งานลำบากพอสมควร (เพราะมีมาตั้งแต่อินเทอร์เน็ตยังไม่ฮิต หาเปเปอร์ต้องวิ่งหาห้องสมุด) ก็เลยได้พัฒนาโปรแกรมนี้ขึ้นมา

หลักการของโปรแกรมนี้เหมาะมากสำหรับการค้นหาข้อมูลทางอินเทอร์เน็ตครับ โดยโปรแกรมนี้จะฝังตัวเป็นส่วนเสริมไปกับโปรแกรมเล่นอินเทอร์เน็ตที่มีชื่อว่า Firefox (ไม่รู้ว่ารู้จักกันหรือเปล่า แต่พูดง่ายๆ คือเป็นโปรแกรมเปิดอินเทอร์เน็ตอันนึง นอกเหนือจาก Internet Explorer หรือตัว e สีฟ้าที่นิยมใช้นะครับ) เวลาเราไปเจอเปเปอร์ไหนน่าสนใจ หรือแม้แต่เจอหน้าอินเทอร์เน็ตไหนน่าสนใจ ก็เพียงคลิ๊กที่ไอค่อน มันก็จะทำการแยกแยะให้เราเสร็จว่าเปเปอร์นั้นคนเขียนชื่ออะไร ลงใน Journal ไหน ปีไหน ในฐานข้อมูลส่วนตัวของเราให้เรียบร้อย หลังจากนั้นเวลาเราจะเอาไปใส่ใน Word ก็เพียงคลิ๊กเดียวอีกเช่นกัน

อะไรมันจะสะดวกปานนั้นใช่ไหมครับ งั้นเราลองกันเลยดีกว่า

ขั้นแรก ก็ให้ติดตั้งโปรแกรม Firefox ตัวหลักก่อน บางท่านอาจจะลงไว้แล้ว แต่ถ้ายังไม่ได้ลง ให้เข้าไปที่ http://www.getfirefox.com นะครับ แล้วก็ดาวน์โหลดมา หลังจากนั้นทำตามขั้นตอนดาวน์โหลดจนเสร็จ (มีเป็นภาษาไทยด้วย) ถ้างง ไม่เข้าใจ ลองอ่านอธิบายวิธีติดตั้งเป็นภาษาไทยโดยละเอียดที่ http://www.mhafai.com/2007/06/firefox-installation-guide นะครับ

พอติดตั้งเสร็จ เปิด Firefox ขึ้นมาก็จะเป็นแบบนี้ครับ:

วิธีการก็เหมือนกันกับการท่องอินเทอร์เน็ตโดยทั่วไปครับ พิมพ์ที่ๆ จะไปด้านบน แต่วันนี้เราจะลงส่วนเสริม Zotero กัน เพราะฉะนั้นก็ไปเลยที่ http://www.zotero.org

หลังจากนั้นแล้ว ให้คลิ๊ก download ด้านขวาบนเพื่อติดตั้ง Zotero ลงใน Firefox ครับ (แนะนำว่าให้ใช้รุ่น 1.0 ก่อนเนื่องจากรุ่น 1.5 นั้นยังไม่เสร็จสมบูรณ์ครับ

หลังจากคลิ๊กถ้ามีช่องเหลืองๆ ด้านบนขึ้นมาถามว่ายอมให้ติดตั้งหรือเปล่า ก็ให้กด ยอมไปครับ

รอสักพัก จะขึ้นว่า ต้องการติดตั้งจริงๆ นะ ก็ให้ติดตั้งไปเลยครับ

หลังจากนั้นโปรแกรมจะทำการดาวน์โหลด Zotero มาใส่ใน Firefox ให้โดยอัตโนมัติครับ (ประมาณ 1 เมกะไบต์กว่าๆ) และเมื่อโหลดเสร็จก็จะให้เราเริ่ม Firefox ใหม่ครับ ก็คลิ๊กเลย

พอเปิดมาใหม่ ทีนี้ทุกหน้าต่างของ Firefox ก็จะมีไอคอน zotero อยู่มุมขวาล่างแล้วครับ

ทีนี้ก็มาถึงวิธีการใช้อย่างจริงจังแล้วครับ จะลองคลิ๊กไอคอนนั้นเข้าไปดูกันเลย (คลิ๊กคำว่า zotero เพื่อเปิดหรือปิดหน้าจอของ Zotero)

ตรงด้านซ้ายนี้จะเป็นรายการที่เราสามารถจัดเป็นหมวดหมู่ได้ครับ เช่น ผมมีเรื่องสนใจด้านหูคอจมูก ก็แยกหูไว้โฟลเดอร์นึง จมูกไว้อีกอันนึง เป็นต้น แต่จะไม่แยกเป็นหมวดหมู่ก็ได้ ทุกอันก็จะไปกองกันอยู่ตรง Library หมด ส่วนตรงการนั้นจะเป็นรายการทั้งหมดในโฟลเดอร์ที่มีในขณะนั้นครับ และด้านขวานั้นจะเป็นรายละเอียดของตรงกลางที่ได้เลือกเอาไว้ครับ

เอาละครับ คราวนี้ถึงเวลาเพิ่มเปเปอร์ลงไปใน Library กันแล้ว ผมขอลองกับเว็บไซต์เดิมๆ ละกัน สมมุติว่าผมหาคำว่า ‘tinnitus’ ใน PubMed โดยใช้ MeSH Term อยู่ (ใครงงว่า MeSH Term คืออะไรกรุณาอ่านที่ผมเขียนไว้คราวก่อนนะครับ

สมมติว่าผมสนใจอันที่สอง ก็เลยคลิ๊กเข้าไปอ่านดู

แล้วก็พบว่ามันใช่เลย! ผมต้องการอันนี้แหละ ที่จะไปใส่ใน Reference ของบทความใหม่ของผม ผมก็เลยคิดว่าจะเอามันไปใส่ใน Library วิธีการง่ายนิดเดียวครับ คือรอให้มันมีไอคอนปรากฎอยู่ข้างๆ แถบรายการข้างบน แล้วก็คลิ๊กตรงรูปเอกสารเล็กๆนั่นแหละ:

Zotero ก็จะแจ้งขึ้นมาว่ามันกำลังเอาเข้าไปใน Library อยู่ รอสักครู่แล้วเช็คดูว่ามันเข้าไปได้ดีหรือเปล่า เพียงเท่านี้เป็นอันจบพิธีครับ จะเห็นว่าเข้าไปอยู่ใน Library เรียบร้อย แล้วก็กรอกตามช่องให้เสร็จเลยด้วย!!

นอกจากนี้เวลาที่มันเป็นรายการหลายๆ อันในหน้าเดียว มันก็ยังจะขึ้นเป็นรูป Folder ให้เราเลือกได้ด้วยนะครับ เช่น ตอนที่เราเห็นผลการค้นหาใน PubMed หลายๆ อัน จะเอาอันไหนก็ติ๊กเลย

เวลาเราต้องการใส่ Citation นั้นเราสามารถคลิ๊กขวาใน Library (จะเลือกหลายๆ อันก็ได้ ให้กด Ctrl ค้างไว้แล้วเลือกหลายๆ อัน) แล้วเลือก Create Bibliography from Selected Items

 

แล้วเลือกว่าต้องการแบบไหน (โดยปกติที่นิยมใช้กัน แนะนำแบบ Vancouver ครับ หรือแบบอื่นๆ ก็มีเช่นของ NLM, AMA) แล้วก็เลือกว่าจะเอาออกไปที่ไหน ถ้าจะเอาไป Paste ในที่อื่น เช่นเขียนลงบล็อกก็เลือก Clipboard เพียงเท่านี้ ก็เสร็จแล้วครับ .. เฮ้ย อะไรมันจะง่ายปานนั้น!

เท่านี้ยังไม่พอนะครับ เนื่องจากว่าคนส่วนใหญ่ไม่ได้เอาไปตัดแปะประกอบการเขียนลงบล็อกแบบผมซะที่ไหน ส่วนมากเขาก็เอาไปประกอบเปเปอร์ตัวเองกันทั้งนั้น แล้วคนส่วนใหญ่ก็ใช้ Word เวลาพิมพ์ไปพิมพ์มาเดียวก็แก้ ย้าย Reference ไปไว้บทแรกมั่ง บทหลังมั่ง บรรทัดก่อนหน้าบ้าง บรรทัดสุดท้ายบ้าง ครั้นจะมานั่งเลือกแต่ละอันทีละ 1 2 3 คงลำบาก แต่ไม่ต้องห่วงครับ ถึงแม้คุณจะใช้ Word คุณก็สามารถใช้ Zotero ติดตามไปได้ด้วย!

เพียงแค่เข้าไปที่เว็บ Zotero ตามเคยครับ มองถัดมาล่างๆ หน่อย จะมีคำว่า Cite from within Word and OpenOffice เพียงคลิ๊กเข้าไปก็จะมีให้ดาวน์โหลดส่วนเสริมสำหรับ Microsoft Word แล้วครับ (ลิงก์มันอยู่ล่างๆ หน่อยนะครับ)

เมื่อโหลดมาลงเสร็จแล้วนั้นเวิร์ดของเราจะปรากฎไอคอนขึ้นมาแถบนึงครับ (แบบของ Word XP, 2003, 2007 อาจต่างกันเล็กน้อยนะครับ)

โดยถ้าเราต้องการใส่อันไหนลงไปใน Word เราก็คลิ๊กไอคอนแรกครับ (ครั้งแรกที่เริ่มใส่ มันจะถามก่อนว่าจะใส่แบบไหน เช่นเคยแนะนำ Vancouver ครับ) แล้วก็จะปรากฎหน้าคล้ายๆ ใน Library ขึ้นมา ก็เพียงแค่เลือกแล้วกด OK เท่านั้นครับ

 

จะใส่ก็อันก็ได้ครับ ตามสบายเลยครับ และถ้าต้องการปิดท้ายด้วยการใส่ Citation ทั้งหมด ก็เพียงคลิ๊กปุ่มที่สามครับ ก็จะมาให้เรียบร้อย

ถ้ามีการโยกย้ายที่เราทำ Citation เอาไว้ ตัวเลขมันจะไม่เปลี่ยนตาม ให้คลิ๊กที่ปุ่มรูปลูกศรทีนึงเพื่อให้มันเปลี่ยนตามครับ

นอกจากจะเอารายการเข้าผ่านทาง PubMed แล้ว เราก็ยังเอาเข้าได้จากเว็บอื่นๆ ด้วยครับ นอกจากนี้แล้วยังใส่รายการได้เองด้วย ลองเล่นๆ ดูได้ครับ แต่ที่ผมใช้ประจำก็จาก PubMed นี่หละ

หวังว่าคงจะมีประโยชน์บ้างนะครับ อย่าลืมนะครับ การที่ไม่ได้ Cite ที่มาของข้อมูลนั้นนอกจากจะทำให้เปเปอร์เราไม่มีน้ำหนักแล้วยังจะไม่ให้เกียรติคนที่เขียนให้เราอ่านกันด้วยครับ ขอให้โชคดีครับ

Incidence and Prevalence

วันนี้ผมขอคั่นด้วยเรื่องง่ายๆ ที่หลายคนอาจจะยังไม่ทราบนะครับ คือเรื่องของ Incidence และ Prevalence เพราะหลายคนอาจจะสับสนกันบ่อยว่ามันคืออะไร ต่างกันยังไง

มาดูคำง่ายกันก่อน นั่นคือ Prevalence คำนี้ความหมายไม่ยากครับ มันก็คือสัดส่วนของคนที่เป็นโรคที่เราสนใจในคนทั้งหมดนั่นเอง หรือภาษาชาวบ้านก็คือ โรคนี้มันเป็นกันกี่ % เช่น เราบอกว่า ในคนไทยมี prevalence ของโรคเบาหวาน 20% ก็หมายความว่า ถ้า ณ วันนี้เอาคนไทยมา 100 คนแบบสุ่มๆ จะพบว่ามีคนเป็นเบาหวาน 20 คนนั่นเอง อันนี้คิดว่าทุกคนคงจะเข้าใจกันดีนะครับ ที่มาของตัวเลขนี้ส่วนมากก็เกิดจากการทำการศึกษาแบบ Cross-sectional นั่นเอง เช่น กระทรวงสาธารณสุขให้โรงพยาบาลทั้งประเทศรายงานจำนวนคนที่เมาในคนที่มารพ. เป็นต้นครับ

สังเกตุว่าเนื่องจากเป็น Cross-sectional มันก็จะเป็นที่ ณ จุดใดจุดหนึ่งของเวลา จึงไม่จำเป็นจะต้องเอาเวลามาเกี่ยวข้องกับการคิด หรือหน่วยเลยครับ ลองดูรูปภาพนี้นะครับ

สังเกตว่า Prevalence ก็คือการตัดเอาที่จุดเวลา ถ้าผมเลือกว่าจุดเวลาของผมคือ 2003 ดังนั้นผมก็ไม่ต้องสนใจเวลาอื่น Prevalence ของคนสีแดง (ไม่เกี่ยวกับการเมืองนะ) = 3 ในคนทั้งหมด 7 คน หรือคิดเป็น 3/7 = 0.43 หรือ 43% นั่นเองครับ

ลองคิดดูนะครับว่าจากรูปดังกล่าว Prevalence ของคนสีแดงที่ปี 2005 เป็นเท่าไหร่

.

.

.

เฉลย คือ 3/7 เหมือนกันนะครับ

นอกจากคำว่า Prevalence ที่ใช้โดยทั่วไปแล้ว ยังมีคำว่า Point Prevalence, Prevalence Proportion, Prevalence Rate ซึ่งต่างก็หมายถึง Prevalence เหมือนกันทั้งหมดครับ (ดังนั้นก็จำคำว่า Prevalence อย่างเดียวก็น่าจะพอ)

ในทางกลับกัน คำว่า Incidence นั้นมีที่มาจากการศึกษาแบบ Cohort ดังนั้นจึงมีเวลาเข้ามาเกี่ยวข้อง โดยหมายถึง จำนวนเคส ใหม่ๆ ที่เกิดขึ้นในช่วงที่เราตามไปศึกษานั่นเอง ยกตัวอย่างรูปเดิมนะครับ

สังเกตุว่าเมื่อเราตามคนที่มีโอกาสเสี่ยงจะเป็นโรค (Population at risk -- ซึ่งแน่นอนคนที่เป็นโรคไปแล้วเราก็ไม่คิด) ไปเป็นระยะเวลา 20 คนปี เราจะเจอเคสใหม่ 2 เคส หรือเราอาจบอกว่าเจอ 2 เคสใน 20 คนปีก็ได้

ทำไมต้องเป็นหน่วย คนปี? เพราะว่ามันจะช่วยเราในการเอาไปเปรียบเทียบกับกลุ่มที่ศึกษาในจำนวนคนหรือปีต่างกันครับ เช่น แทนที่จะศึกษา 5 คนใช้เวลา 4 ปีแบบตัวอย่าง เราอาจจะศึกษา 10 คนในเวลา 2 ปี ก็ได้ 20 คนปีเหมือนกันเลย

ดังนั้น ตามคน 5 คนไป 4 ปี พบ 2 เคส ก็ = 2/20 = 0.1 Case/person-year
ตามคน 10 คนไป 2 ปี พบ 2 เคส ก็ = 2/20 = 0.1 Case/person-year
ตามคน 100 คนไป 0.2 ปี พบ 2 เคสก็ = 2/20 = 0.1 Case/person-year เหมือนกันหมด

เพราะฉะนั้นก็จะเห็นว่า มันจะมีเวลาเข้ามาเกี่ยวข้องด้วยนั่นเองครับ ดังนั้นเวลาไปใช้ที่ไหน ใช้ให้ถูกหน่อยนะครับ Prevalence ไม่ต้องมีหน่วยของเวลา แต่ถ้า Incidence นั่นต้องมีแน่ๆ อย่าใช้สับสนกันนะครับ

Understanding Risk

“ความเสี่ยง” นั้นเป็นเรื่องยากที่จะอธิบายให้เข้าใจได้ง่ายๆ แต่ส่วนใหญ่แล้วเรามักจะพูดถึงอัตราการเกิดโรคต่างๆ นั้นเป็นความเสี่ยงครับ

พอดีช่วงนี้ยุ่งนิดหน่อย แต่ไปเจอเว็บไซต์รายงานข่าวของ BBC News ที่พูดเรื่องเกี่ยวกับความเสี่ยงดังกล่าวเป็นกราฟฟิคที่เข้าใจง่ายๆ เลยมาลองให้ดูกันครับ

เข้าไปดูที่ BBC News กันเลยครับ: How to understand risk in 13 clicks.

Precision, Accuracy, Bias, Chance

วันนี้พักเรื่องสถิติ มาคุยกันเรื่องความเที่ยงตรงและความแม่นยำกันนะครับ

หนึ่งในเรื่องที่น่าสนใจของการทำการศึกษาก็คือเรื่องของ ความผิดพลาดที่เกิดจากการศึกษา ทุกคนคงทราบดีว่ามันไม่สามารถที่การศึกษาใดๆ จะทำนายผลลัพธ์ได้ตรงเผง 100% ดังนั้นมันจึงเกิดคำว่า Error ขึ้นมาครับ

คำว่า Error นั้นเป็นคำรวมๆ หมายถึงความผิดพลาดที่เกิดขึ้น ซึ่งอาจเกิดจากความตั้งใจหรือไม่ตั้งใจก็ได้ครับ ในทางระบาดวิทยาและสถิติแล้ว เราแบ่งความผิดพลาเป็นสองแบบใหญ่ๆ คือ

• ความผิดพลาดที่เกิดขึ้นอย่างไม่เป็นระบบ (Non-Systematic Error หรือที่เรียกว่า Random Error) บางคนเรียกว่า Chance
• ความผิดพลาดที่เกิดขึ้นเป็นระบบ (Systematic Error) หรือที่เรียกว่า Bias

พูดมาตรงนี้ก็อาจจะงงเล็กน้อย ผมจะลองอธิบายด้วยวิธีที่หนังสือส่วนใหญ่ใช้ นั่นก็คือ เกมปาเป้าครับ

ในเกมปาเป้านั้นจุดมุ่งหมายก็คือพยายามทำให้ลูกดอกนั้นเข้าตรงเป้ามากที่สุด เหมือนกันกับที่เราทำวิจัย เราก็มีจุดมุ่มหมายทำให้ผลลัพธ์ที่เกิดขึ้นนั้นตรงกันกับความเป็นจริงในธรรมชาติมากที่สุดเหมือนกัน

อย่างไรก็ตาม ทุกคนที่ปาเป้าก็คงเข้าใจว่าถึงจะปาให้ดียังไง ก็คงไม่สามารถจะตรงเป้าตลอดกาลได้ (ยกเว้นคุณจะแม่นมากๆ แต่คงจะมีไม่กี่คนที่แม่นเป๊ะขนาดนั้น) สมมุติว่าปาไปสี่ดอก มันก็คงจะไม่ลงตรงจุดเดียวกันเสียทีเดียว คงมีเบี้ยวไปข้างซ้ายบ้าง เบี้ยวไปขวาบ้าง

นี่ละครับคือที่มาของคำว่า Random Error (Chance) นั่นก็คือว่าไม่ได้มีใครอยากที่จะให้มันเกิด แล้วเวลามันเกิดแล้วมันก็มีโอกาสไปได้ทุกๆ ด้าน ทั้งด้านบน ด้านล่าง ด้านซ้าย หรือด้านขวา

แต่หากว่ามีคนสายตาเอียงมาปา ลองนึกภาพดูว่ามันจะเกิดอะไรขึ้นนะครับ

จะเห็นว่าเพราะเขาตาเอียง ถึงแม้ว่าจะแม่นเพียงไหน เขาก็จะปาเบี้ยวไปตลอดทุกที

ความเที่ยงตรง (Precision) นั้นก็เปรียบได้กับในการปาลูกดอกในแต่ละครั้ง ว่ามันจะเบี้ยวซ้าย เบี้ยวขวาไปสักเท่าไหร่ (มันจะ Precise ได้สักเท่าไหร่) ยิ่งปาเก่ง ฝึกบ่อย มันก็จะทำให้เที่ยงตรงมากขึ้นเรื่อยๆ บางคนเรียกว่า มันสามารถจะทำซ้ำ แล้วผลลัพธ์ออกมาแบบเดิมได้ซักเท่าไหร่ (Reproducability/Repeatablility) หรือจะพูดย้อนไปคือ มันมี Random Error ซักแค่ไหนกัน

สำหรับความแม่นยำ หรือ Accuracy  นั้นก็คือมัน “ตรงเป้า” ซักแค่ไหน คือคนปาเนี่ยสายตาเอียงหรือเปล่า ถ้ามีอะไรมาบังตา ก็จะทำให้ความแม่นยำนั้นลดลง เปรียบได้กับว่าแว่นนั้นคือ Bias ที่ทำให้ลูกดอกที่ปาออกไปมันผิดปกติไปในทางเดียวกัน

หนังสือหลายเล่มจะแสดงรูปสี่รูปต่อไปนี้ครับ:

นั่นก็คือ จากรูปบนซ้าย จะเห็นได้ว่านักปาเป้านั้นทั้งซ้อมบ่อย แล้วก็ไม่ตาเอียง (Random error น้อย, ไม่มี Bias)

ส่วนรูปบนขวานั้นซ้อมบ่อยจริง แต่ดันตาเอียง (Random error น้อย แต่ดันมี Bias)

ในทางกลับกันรูปล่างซ้ายนั้นซ้อมไม่บ่อย แต่โชคดีที่ตายังไม่เอียง (Random error เยอะกว่า แต่โชคดีที่ไม่มี Bias)

และรูปล่างขวานั้นคงไม่มีใครอยากให้เกิด เพราะนอกจากจะอ่อนซ้อมแล้วยังตาเอียงไปทางขวาอีก -_-“ (นั่นคือมีทั้ง Random error เยอะ และมีทั้ง Bias อีกต่างหาก)

หรือถ้าผมจะเรียงให้ดูมันก็จะเป็นไปตามนี้ครับ:

 

สำหรับ Bias ที่เกิดขึ้นนั้นเกิดได้จากหลายสาเหตุครับ ไว้โอกาสหน้าจะมาอธิบายต่อครับ

ใช้โปรแกรม R ช่วยคำนวณ Odds Ratio

มีหลายคนเมล์มาถามผมเกี่ยวกับการคำนวณ Odds Ratio ที่ได้จากการศึกษา วันนี้ผมขอแนะนำโปรแกรมทางสถิติตัวหนึ่งที่นักสถิติและนักระบาดวิทยาหลายคนชอบใช้ นั่นคือโปรแกรม R ครับ

หลายท่านคงเคยได้ยินโปรแกรม SPSS (ซึ่งย่อมาจาก Statistical Package for the Social Sciences) มาแล้ว แต่ท่านทราบหรือไม่ ว่าท่านอาจจะกำลังใช้โปรแกรมนี้อย่างผิดกฎหมายอยู่! นั่นเป็นสิ่งที่ไม่ดีเลยครับ เรามาใช้โปรแกรมอื่นทดแทนโปรแกรมที่ผิดลิขสิทธิ์กันดีกว่า

โปรแกรม R นี้พูดแล้วก็เปรียบเสมือนเครื่องคิดเลขหนึ่งอันครับ โปรแกรมนี้สร้างโดยนักสถิติชาวนิวซีแลนด์ชื่อ Ross Ihaka และ Robert Gentleman ทั้งสองท่านนี้เห็นว่าโปรแกรมสถิติที่เราๆ ท่านๆ ใช้กันอยู่นั้นส่วนใหญ่จะมีราคาแพงถึงแพงหูฉี่ ก็เลยลองเขียนโปรแกรมขึ้นมาใช้เองดู และยังเผยแพร่โค้ดโปรแกรมออกมาอีกด้วย

เนื่องจากเป็นโปรแกรมที่สามารถดาวน์โหลดมาใช้ได้ฟรี ก็อาจจะไม่มีการรับประกันใดๆ อย่างไรก็ตาม โปรแกรมนี้เป็นโปรแกรมที่ได้รับการยอมรับจากนักสถิติทั่วโลกเลยทีเดียวครับ (Paper หลายอันใช้โปรแกรมนี้ในการคำนวณ)

พูดมานานแล้ว มาโหลดไปใช้กันดีกว่า เข้าหน้านี้ (http://www.r-project.org/) แล้วเลือกทำตามขั้นตอนต่อไปนี้เลยครับ

1. เลือก Download ใต้หัวข้อ CRAN
2. เลือกสถานที่ที่ใกล้เราที่สุดเพื่อจะได้โหลดเร็วๆ (เมืองไทยก็มี) แต่แนะนำ Australia เพราะเมืองไทยมักไม่อัพเดต

3. เลือกวินโดวส์ ถ้าคุณใช้วินโดวส์
4. เลือก base
5. เลือกอันที่ลงท้ายด้วย .exe ครับ (มันจะเป็นชื่อเวอร์ชั่นอยู่เช่นขณะที่ผมเขียนอยู่นี่มัน 2.8.1)

6. ได้มาแล้ว ลงตามปกติเลยครับ

เมื่อเปิดโปรแกรมจะพบหน้าตาโปรแกรมดูโบราณๆ นิดนึง (เห็นโบราณแบบนี้แต่มันทรงพลังทีเดียวเลยล่ะ)

สามารถลองพิมพ์ลงไปได้เลยครับว่าอยากจะให้มันคำนวณอะไร แล้วก็กด Enter

ถ้าพิมพ์ผิดไม่ต้องกลัวมันไม่เจ๊งครับ มันก็แค่ขึ้น Error เท่านั้นแหละ แต่ถ้าพิมพ์ๆ ไปแล้วเป็นแบบนี้

> log(log(4)+sqrt(5)
+ |

นั่นเกิดจากว่าคุณใส่สูตรไม่จบ ส่วนมากเกิดลืมใส่วงเล็บ ก็แค่พิมพ์ ) เพิ่มไปแล้วกด Enter มันก็จะคำนวณให้ครับ

ฟังก์ชันที่ใช้นั้นก็มีหลากหลาย ตั้งแต่ธรรมดาๆ เชน log, sqrt (ย่อมาจาก square root), sin, cos, tan,… จนไปถึงฟังก์ชันทางสถิติเช่นพวกหา p-value จากค่า Chi-square เลยทีเดียวครับ (จนตอนนี้ผมใช้แทนเครื่องคิดเลขไปแล้วแหละ)

หมายเหตุนิดนึงว่าฟังก์ชัน log นั้นเป็นฐาน e นะครับ ถ้าต้องการฐานสิบ ก็พิมพ์ ,10 ในวงเล็บแบบนี้

> log(1,10)
[1] 0

สำหรับเลข [1] นั้นไม่ต้องสนใจครับ เขาใช้เวลามันมีผลลัพธ์เยอะๆ ขึ้นบรรทัดใหม่มันจะบอกว่าเป็นผลลัพธ์อันที่เท่าไหร่

ข้อดีของโปรแกรม R นี้นอกจากจะฟรีแล้วยังสามารถใส่ความสามารถอื่นๆ เข้าไปได้ ในวันนี้ที่ผมจะเอามาใช้คำนวณ Odds Ratio นั่นคือโปรแกรมเสริม EpiCalc โดยอาจารย์วีระศักดิ์จากมอ. เขียนไว้สำหรับทำงานด้านระบาด โดยเฉพาะเลยครับ

วิธีลงโปรแกรม Epicalc เพิ่มให้เราเลือกจากเมนูดังนี้

1. เลือก Packages –> Install Package(s)…
2. เลือกประเทศไหนก็ได้เหมือนเดิม (แนะนำ Australia เหมือนเดิมครับ)
3. จะเจอโปรแกรมเสริม (เรียกว่า package) มากมายก่ายกอง ให้เลือก epicalc ที่เราต้องการ

4. มันจะดาวน์โหลดมาให้เอง รอนิดนึงครับ

5. ดาวน์โหลดเสร็จแล้วยังใช้ไม่ได้ ต้องเลือก Load package… เพื่อเอามาใช้ก่อน
6. แล้วเลือก epicalc เหมือนเดิม

สำหรับขั้นที่ 5-6 นั้นต้องทำทุกครั้งหลังเปิดโปรแกรมใหม่นะครับ เอาละครับ ทีนี้มาลองใส่ข้อมูลกันเลยนะครับ

สมมติว่าผมทำการศึกษาคนไข้กลุ่มหนึ่ง โดยแบ่งคนไข้หูอักเสบเป็นสองกลุ่ม กลุ่มนึงให้หยอดยา อีกกลุ่มหยอดน้ำธรรมดา แล้วลองดูซิว่าทั้งสองกลุ่มหายหรือไม่หาย

ในที่นี้ exposure คือการหยอดยา (exposure +) หรือไม่หยอดยา (exposure –) และ outcome ที่ผมสนใจคือหูยังเป็นโรคอยู่ (outcome +) หรือหูไม่เป็นโรคแล้ว (outcome –) ถ้าเขียนตารางก็ได้ดังนี้ครับ

แต่แทนที่เราจะมานั่งคำนวณเอง เราก็สามารถใช้โปรแกรม R+Epicalc นี้คำนวณได้ โดยใส่ฟังก์ชันดังนี้

> csi(3,29,18,13)

          Exposure
Outcome    Non-exposed Exposed Total
  Negative 13          29      42  
  Positive 18          3       21
  Total    31          32      63

           Rne         Re      Rt  
  Risk     0.58        0.09    0.33 
                       Estimate Lower95ci Upper95ci
Risk difference (Re - Rne) -0.49    -0.72     -0.25   
Risk ratio                0.16     0.06      0.41    
Protective efficacy =(Rne-Re)/Rne*100  
                           83.9     59.14     93.73   
   or percent of risk reduced
Number needed to treat (NNT)2.05   1.39      3.97    
   or -1/(risk difference)                                          

เราก็จะได้มาหมดเลย อย่างในที่นี้ที่จะรายงานก็คือ Relative Risk (Risk Ratio) = 0.16 โดยมี 95%CI = 0.06-0.41 ครับ

ถ้าจำไม่ได้ว่าในวงเล็บอันไหนเป็นอันไหน ก็ลองพิมพ์ดู แล้วดูว่าตารางนั้นออกมาตรงหรือเปล่าก็ได้ครับ แต่ถ้าอยากรู้คำสั่งให้มากขึ้น ให้พิมพ์

> help(csi)

จะขึ้นข้อความช่วยเหลือให้ครับ

ลองใช้กันดูนะครับ ผมหวังว่าจะมีประโยชน์ ถ้าว่างวันหลังจะมาเขียนเพิ่ม